---------------------------------------------------------------------------------------------------------------
ELMÉLETI FIZIKA/MECHANIKA
(Vizsgakérdések)
---------------------------------------------------------------------------------------------------------------
1.)
A természettudományok „megismerési módszerei”: induktív-deduktív módszer, modellalkotás, a korrespondencia elv.
Egyetlen tömegpont görbe vonalú mozgásának a leírása. Newton axiómák.
2.)
Egyetlen tömegpont dinamikája. Az impulzus tétel. A munkatétel. Konzervatív erők. A mechanikai energia megmaradás tétele. A tömegpont perdülete és a perdülettétel. Mozgás centrális erőtérben. Az effektív potenciál(is energia) és a pálya alakja.
3.)
A lineáris (mechanikai) oszcillátor vizsgálata. A csillapítások osztályozása és a mozgás jellegzetességei. A gerjesztett oszcillátor vizsgálata A kauzalítás elve. A Dirac-delta gerjesztés. Dirac-delta disztribúció főbb sajátosságai.
4.)
A lineáris rendszerek vizsgálatának alapjai. Gerjesztések és válaszfüggvények. A Green- függvény. A Fourier-analízis alapjai. A Fourier-integrál és a Fourier-transzformáció. A Green-függvény Fourier-transzformáltja. A Fourier-transzformáció tulajdonságai.
5.)
Tömegpontrendszer dinamikája. A tömegközéppont tétele. A tömegpontrendszer impulzusa és az impulzus tétel.. Tömegpontrendszer perdülete és a perdülettétel.
6.)
Tömegpontrendszer energiája és a munkatétel. Megmaradási törvények: impulzus, perdület, energia. Szimmetriák.
7.)
A merev testek dinamikája. Rögzített tengely körüli forgás. A perdület és a tehetetlenségi nyomaték (tenzor). A „szabad” tengely fogalma. A forgó merev test mozgási energiája. Rögzített pont körüli mozgás, Euler-egyenletek. A precesszió.
8.)
Deformálható közegek mozgásának a dinamikája. A deformációs tenzor, ill. mátrix elemeinek fizikai jelentése. Erőhatások folytonos anyageloszlású testekben. A feszültség tenzor, ill. mátrix elemeinek fizikai jelentése. A mérlegegyenletek általános megfogalmazása folytonos anyageloszlású közegekben. A szubsztanciális derivált fogalma.
9.)
Folytonos anyageloszlású testek (közegek) dinamikája. A Lagrange-féle és az Euler-féle szemlélet és a mozgásegyenletek megfogalmazása. A mozgásegyenlet, mint impulzus- mérleg.
10.)
Folytonos anyageloszlású testek (közegek) dinamikája.
Az energia mérlegegyenlete és a forrástagok általános fizikai jelentése.
Konkrét példák: 1. rugalmas közegek,
2. reális folyadékok.
11.)
Rugalmas közegek dinamikája. A rugalmas munka és a belső energia-sűrűség fogalma. A stabil egyensúlyi állapot és a rugalmassági állandók bevezetése. Folytonos, homogén, izotróp anyag) rugalmassági állandói (Lamé-együtthatók). A Hooke-törvény. A mozgásegyenletek általános megadása. A hullámegyenletek. a Hooke-törvény..
12.)
Folyadékok és gázok termodinamikai jellemzése. Az ideális folyadék fogalma és az Euler-féle mozgásegyenlet. Az áramvonal fogalma, Bernoulli- egyenletek.
13.)
Hanghullámok terjedése (összenyomható) rugalmas közegekben.
A reális folyadékok és a Navier-Stokes-egyenlet. A Hagen-Piseuille-törvény. A Reynolds-szám fogalma. A Kármán-féle örvények kvalitatív bemutatása.
14.)
Analitikus mechanika. Variációszámítási problémák. A Lagrange-függvény. A Hamilton-elv és az Euler-Lagrange-egyenletek. A Hamilton-függvény és a kanonikus egyenletek. Poisson-zárójelek. A nagyon nagy részecskeszámú rendszerek és a Liouville-egyenlet.
---------------------------------------------------------------------------------------------------------------------
KÉPLETGYÜJTEMÉNY
----------------------------------------------------------------------------------------------------------------------
![]()
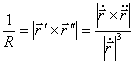
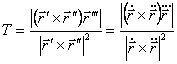

![]()
![]() =
=![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
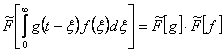
![]()
![]()
![]()
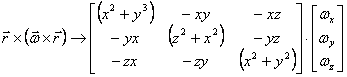
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
---------------------------------------------------------------------------------------------------------------------